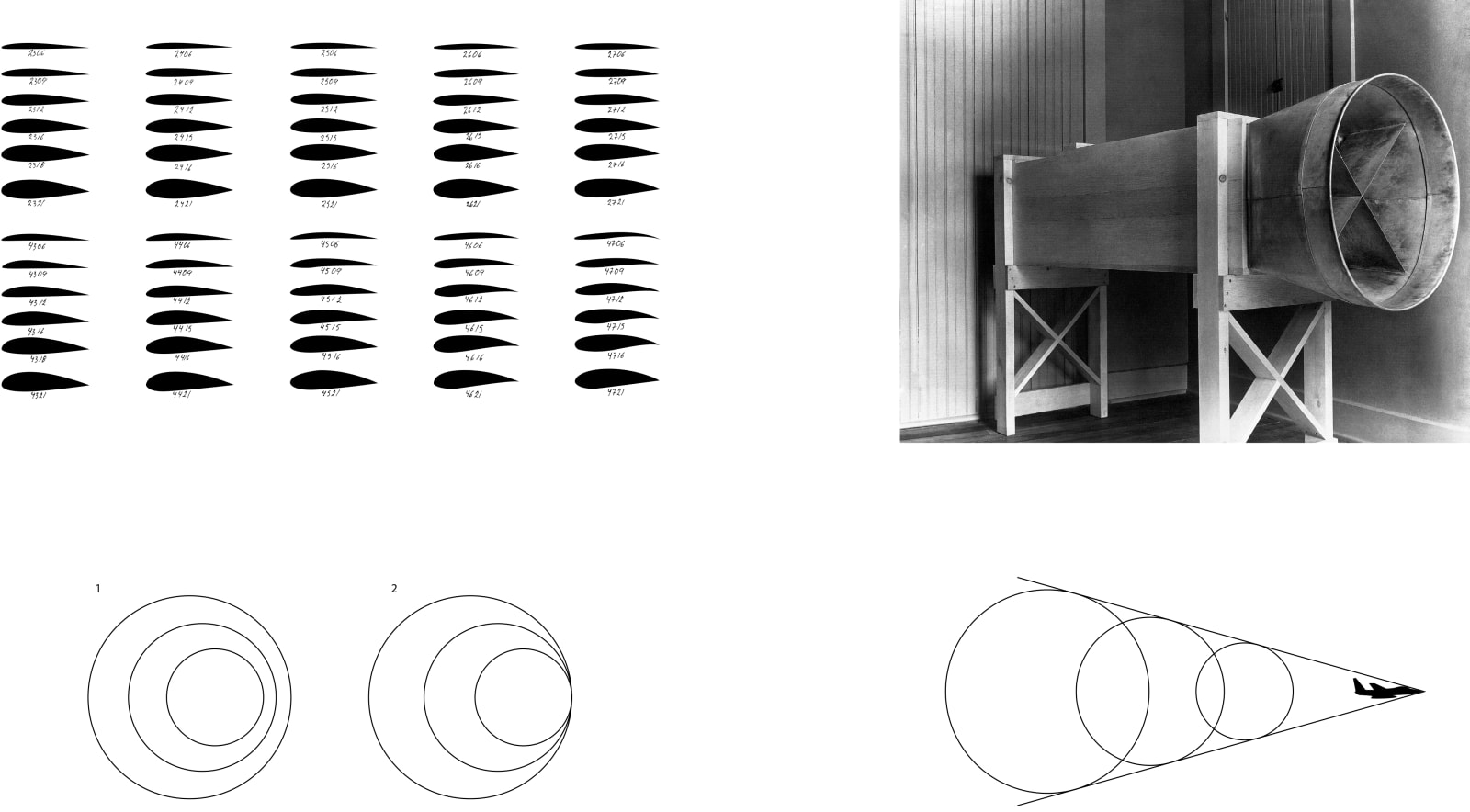
The Wright brothers are synonymous with flight: famous for being the first to invent, construct, and fly an airplane in 1903. In autumn 1901, they built a wind tunnel where they tested countless different wing and airfoil shapes. Using data from their experiments, the brothers successfully designed a glider in 1902 and the Wright Flyer the following year. In the decades that followed, the United States National Advisory Committee for Aeronautics (NACA) was instrumental in systematising and institutionalising modern aviation. Beginning in the 1920's, NACA ran tests with a variable-density aerodynamics at the time. The diagram on the left illustrates different categories of airfoil shapes and sizes, each designated by four numbers: the first digit specifies the maximum camber m in percentage of the chord c; the second digits indicates the position of the maximum camber p in tenths of a chord, and the last two digits provide the maximum thickness t of the airfoil in percentage of the chord. The numbers can be ascertained with the following equations:

Calculate the mean camber line coordinates by plugging the values m and p into the following equations for each of the x coordinates:

Yc = m / p2 (2px - x^2) front (0 ≤ x < p)
Yc = m / (1 - p)^2 [(1 - 2p) + 2px - x^2] back (p ≤ x ≤ 1)

Compute the thickness distribution above (+) and below (-) the mean line by plugging the value of t into the following equation for each of the x coordinates:

± Yt = t / 0.2 (0.2969√x - 0.1260x - 0.3561 x^2 + 0.2843 x^3 - 0.1015 x^4)

Find the final coordinates for the upper (Xu, Yu) and lower (Xl, Yl) surfaces of the airfoil:

Xu = X - Yt sin θ
Yu = Yc + Yt cos θ
Xl = X + Yt sin θ
Yl = Yc - Yt cos θ

The drawings below depict a different element of the relationship between jets and the surrounding air, illustrating high-pressure shock waves generated as one approaches the speed of sounds, and surpasses it.

------
Les frères Wright sont synonymes de vol: ils sont connus pour avoir été les premiers à inventer, construire et piloter un avion en 1903. À l'automne 1901, ils ont construit une soufflerie où ils ont testé d'innombrables formes d'ailes et de pales aérodynamiques. En utilisant les données de leurs expériences, les frères ont conçu avec succès un planeur en 1902 et le Wright Flyer l’année suivante. Dans les décennies qui ont suivi, le Comité consultatif national des États-Unis pour l'aéronautique (NACA) a joué un rôle déterminant dans la systématisation et l'institutionnalisation de l'aviation moderne. À partir des années 1920, le NACA a effectué des tests avec une aérodynamique à densité variable à l'époque. Le diagramme de gauche illustre différentes catégories de formes et de tailles de surfaces portantes, désignées chacune par quatre chiffres: le premier chiffre indique la cambrure maximale m en pourcentage de la corde c; les deuxièmes chiffres indiquent la position de la cambrure maximale p en dixièmes d'une corde et les deux derniers chiffres indiquent l'épaisseur maximale t de la surface portante en pourcentage de la corde. Les nombres peuvent être déterminés avec les équations suivantes:

Calculez les coordonnées moyennes de la ligne de carrossage en insérant les valeurs m et p dans les équations suivantes pour chacune des coordonnées x:

Yc = m / p2 (2px - x^2) front (0 ≤ x < p)
Yc = m / (1 - p)^2 [(1 - 2p) + 2px - x^2] back (p ≤ x ≤ 1)

Calculez la distribution d'épaisseur au-dessus (+) et au-dessous (-) de la ligne moyenne en insérant la valeur de t dans l'équation suivante pour chacune des coordonnées x:

± Yt = t / 0.2 (0.2969√x - 0.1260x - 0.3561 x^2 + 0.2843 x^3 - 0.1015 x^4)

Trouvez les coordonnées finales des surfaces supérieure (Xu, Yu) et inférieure (Xl, Yl) de la surface portante:

Xu = X - Yt sin θ
Yu = Yc + Yt cos θ
Xl = X + Yt sin θ
Yl = Yc - Yt cos θ

Les dessins ci-dessous illustrent un élément différent de la relation entre les jets et l'air ambiant, illustrant les ondes de choc à haute pression générées à mesure que l'on s'approche de la vitesse des sons et les surpassent.