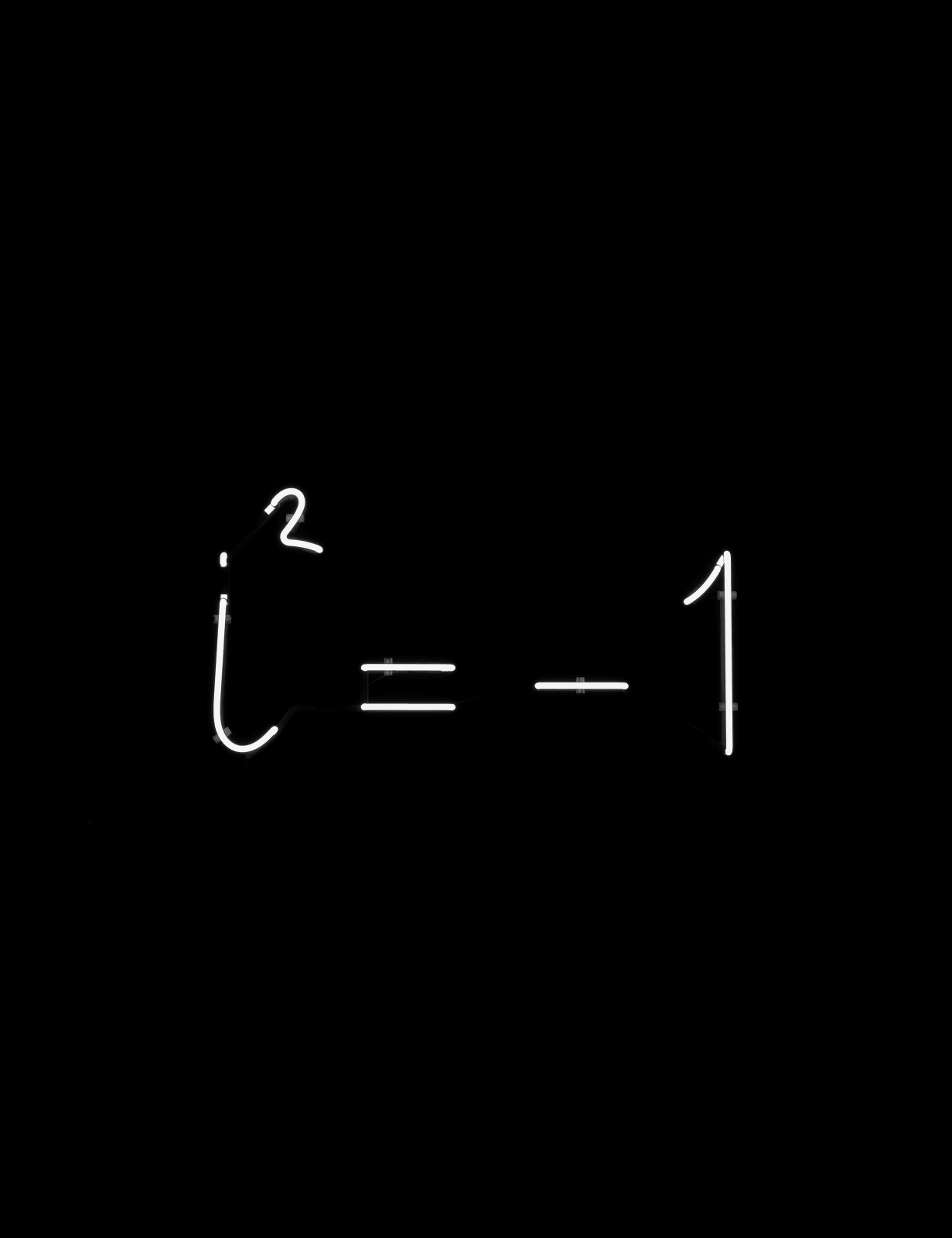Andrea Galvani’s Square Root of -1 reminds us that numbers are constructs of the human mind. They represent—but are not synonymous with—aspects of nature. Very few are aware of how deeply our society depends on numbers that do not represent quantities, lengths, areas, or amounts of money. Yet most modern technology, from electric lighting to digital cameras, could not have been invented without them.

When Girolamo Cardano (1501-1576) encountered a new kind of number in 1545, he had no idea the power of the enigma he found. Cardano was writing a book on algebra and stumbled upon what we now know as “imaginary numbers.” They’re different from real numbers because the square of an imaginary number is always negative. Cardano was baffled, his findings defied all known systems of logic. He dismissed them as “useless.” By 1572, Rafael Bombelli—who was studying Cardano’s text—noticed that although these mysterious entities seemed to make no sense, they could be used in calculations to yield accurate results. The love-hate relationship between mathematicians and imaginary numbers continued for centuries. Gottfried Wilhelm Leibniz eloquently wrote, “The Divine Spirit found a sublime outlet in that wonder of analysis, that portent of the ideal world, that amphibian between being and non-being, which we call the imaginary root of a negative unity.” It wasn’t until the eighteenth century, however, that we were able to figure out what they actually are, and not until the nineteenth century that mathematicians started to feel comfortable using them. Imaginary or complex numbers opened a new domain where the old rules did not apply.